Ecoviability scenarios

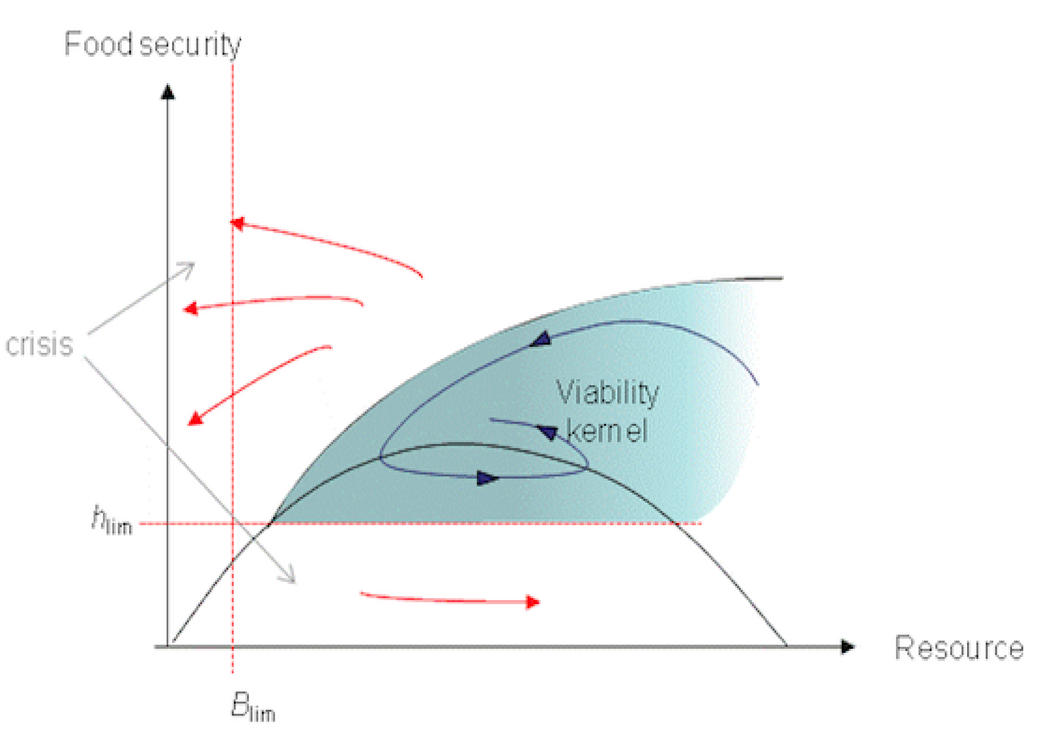
The aim of ecoviability scenarios is to identify states and controls that ensure the ”good health” and safety of socioecosystems. By identifying the viability conditions that allow multiple constraints to be fulfilled over time, considering both present and future states of a dynamic system, the viability scenarios conveys information on sustainability and intergenerational equity. The recent development of probabilistic viability also gives major insights in terms of risks or vulnerabilities management. The constraints underpinning viability can involve ecological thresholds as in the case of an extinction threshold in population viability analysis (PVA). Economics constraints (guaranteed rent, food security) or ecosystem services requirements can also be integrated as in thus allowing for multi-criteria and
bio-economic analyses. The viability kernel exemplified by the figure above plays a pivotal mathematical role in viability analysis. The approach has already been successfully applied to biodiversity valuation and to fisheries management in several contexts including (eco)-system or biodiversity dynamics. In relation to food security, provide useful bio-economic insights in the context of developing countries under important demographic pressure.
In contexts where uncertainties have a probabilistic nature, bio-economic viability can be defined as the fulfillment of constraints with a high enough probability:
where β corresponds to some prescribed confidence rate (99%, 90%, ) and where the probability P is computed with respect to the uncertainty ω.










